If you're anything like me, you've used Excel to plot data, then used the built-in “add fitted line” feature to overlay a fitted line to show the trend, and displayed the “goodness of fit,” the r-squared (R2) value, on the chart by checking the provided box in the chart dialog.
The R2 calculated in Excel is often used as a measure of how well a model explains a response variable, so that “R2 = 0.8” is interpreted as “80% of the variation in the 'y' variable is explained by my model.” I think that the ease with which the R2 value can be calculated and added to a plot is one of the reasons for its popularity.
There's a hidden trap, though. R2 will increase as you add terms to a model, even if those terms offer no real explanatory power. By using the R2 that Excel so helpfully provides, we can fool ourselves into believing that a model is better than it is.
Below I'll demonstrate this and show an alternative that can be implemented easily in R.
Some data to work with
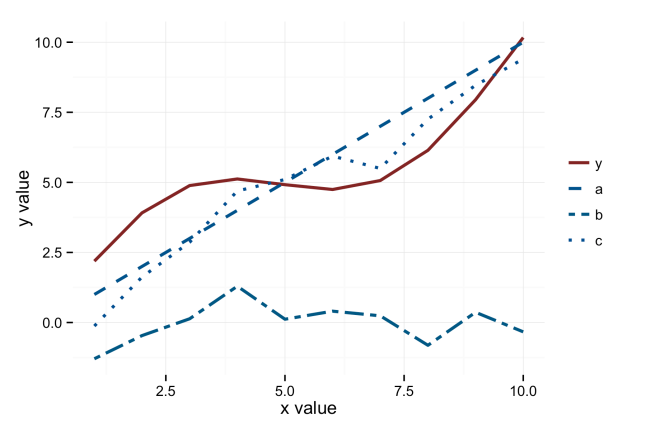
First, let's create a simple, random data set, with factors a, b, c and response variable y.
head(my.df)
## y a b c ## 1 2.189 1 -1.2935 -0.126 ## 2 3.912 2 -0.4662 1.623 ## 3 4.886 3 0.1338 2.865 ## 4 5.121 4 1.2945 4.692 ## 5 4.917 5 0.1178 5.102 ## 6 4.745 6 0.4045 5.936
Here is what this data looks like:
Calculating R-squared
What Excel does when it displays the R2 is create a linear least-squares model, which in R looks something like:
my.lm <- lm(y ~ a + b + c, data = my.df)
Excel also does this when we call RSQ() in a worksheet. In fact, we can do this explicitly in Excel using the Regression analysis option in the Analysis Pack add-on, but I don't know many people who use this, and Excel isn't known for its reliability in producing good output from the Analysis Pack.
In R, we can obtain R2 via the summary() function on a linear model.
summary(my.lm)
## ## Call: ## lm(formula = y ~ a + b + c, data = my.df) ## ## Residuals: ## Min 1Q Median 3Q Max ## -1.2790 -0.6006 0.0473 0.5177 1.5299 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 2.080 0.763 2.72 0.034 * ## a -0.337 0.776 -0.43 0.679 ## b -0.489 0.707 -0.69 0.515 ## c 1.038 0.817 1.27 0.250 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 1.1 on 6 degrees of freedom ## Multiple R-squared: 0.833, Adjusted R-squared: 0.75 ## F-statistic: 10 on 3 and 6 DF, p-value: 0.00948
Since summary() produces a list object as output, we can grab just the R2 value.
summary(my.lm)$r.squared
## [1] 0.8333
Normally, we would (somewhat loosely) interpret this as telling us that about 83% of the variation in the response y is explained by the model.
Notice that there is also an "adjusted r-squared” value given by summary(). This tells us that only 75% of the variation is explained by the model. Which is right?
The problem with R-squared
Models that have many terms will always give higher R2 values, just because more terms will slightly improve the model fit to the given data. The unadjusted R2 is wrong. The calculation for adjusted R2 is intended to partially compensate for that “overfit,” so it's better.
It's nice that R shows us both values, and a pity that Excel won't show the adjusted value. The only way to get an adjusted R2 in Excel is to run the Regression analysis; otherwise, we have to calculate adjusted R2 manually.
Both R2 and adjusted R2 are measures of how well the model explains the given data. However, in industry we usually want to know something a little different. We don't build regression models to explain only the data we have; we build them to think about future results. We want R2 to tell us how well the model predicts the future. That is, we want a predictive R2. Minitab has added the ability to calculate predictive R2 in Minitab 17, and has a nice blog post explaining this statistic.
Calcuting predictive R-squared
Neither R nor Excel provide a means of calculating the predictive R2 within the default functions. While some free R add-on packages provide this ability (DAAG, at least), we can easily do it ourselves. We'll need a linear model, created with lm(), for the residuals so we can calculate the “PRESS” statistic, and then we need the sum of squares of the terms so we can calculate a predictive R2.
Since the predictive R2 depends entirely on the PRESS statistic, we could skip the added work of calculating predictive R2 and just use PRESS, as some authors advocate. The lower the PRESS, the better the model is at fitting future data from the same process, so we can use PRESS to compare different models. Personally, I'm used to thinking in terms of R2, and I like having the ability to compare to the old R2 statistic that I'm familiar with.
To calculate PRESS, first we calculate the predictive residuals, then take the sum of squares (thanks to (Walker’s helpful blog post) for this). This is pretty easy if we already have a linear model. It would take a little more work in Excel.
pr <- residuals(my.lm)/(1 - lm.influence(my.lm)$hat) PRESS <- sum(pr^2) PRESS
## [1] 19.9
The predictive R2 is then (from a helpful comment by Ibanescu on LikedIn) the PRESS divided by the total sum of squares, subtracted from one. The total sum of squares can be calculated directly as the sum of the squared residuals, or obtained by summing over Sum Sq from an anova() on our linear model. I prefer using the anova function, as any statistical subtleties are more likely to be properly accounted for there than in my simple code.
# anova to calculate residual sum of squares my.anova <- anova(my.lm) tss <- sum(my.anova$"Sum Sq") # predictive R^2 pred.r.squared <- 1 - PRESS/(tss) pred.r.squared
## [1] 0.5401
You'll notice that this is smaller than the residual R2, which is itself smaller than the basic R2. This is the point of the exercise. We don't want to fool ourselves into thinking we have a better model than we actually do. One way to think of this is that 29% (83% – 54%) of the model is explained by too many factors and random correlations, which we would have attributed to our model if we were just using Excel's built-in function.
When the model is good and has few terms, the differences are small. For example, working through the examples in Mitsa's two posts, we see that for her model 3, R2 = 0.96 and the predictive R2 = 0.94, so calculating the predictive R2 wasn't really worth the extra effort for that model. Unfortunately, we can't know, in advance, which models are “good.” For Mitsa's model 1 we have R2 = 0.95 and predictive R2 = 0.32. Even the adjusted R2 looks pretty good for model 1, at 0.94, but we see from the predictive R2 that our model is not very useful. This is the sort of thing we need to know to make correct decisions.
Automating
In R, we can easily wrap these in functions that we can source() and call directly, reducing the typing. Just create a linear model with lm() (or an equivalent) and pass that to either function. Note that pred_r_squared() calls PRESS(), so both functions have to be sourced.
pred_r_squared <- function(linear.model) {
lm.anova <- anova(linear.model)
tss <- sum(lm.anova$"Sum Sq")
# predictive R^2
pred.r.squared <- 1 - PRESS(linear.model)/(tss)
return(pred.r.squared)
}
PRESS <- function(linear.model) {
pr <- residuals(linear.model)/(1 - lm.influence(linear.model)$hat)
PRESS <- sum(pr^2)
return(PRESS)
}
Then we just call the function to get the result:
pred.r.squared <- pred_r_squared(my.lm) pred.r.squared
## [1] 0.5401
I've posted these as Gists on GitHub, with extra comments, so you can copy and paste from here or go branch or copy them there.
References and further reading
- Mitsa, T. Use PRESS, not R squared to judge predictive power of regression. 12 May 2013. Analytical Bridge. Accessed 14 May 2014. Shows how r-squared can lead to a misleading interpretation of model fit and provides an explanation of the PRESS statistic, with examples comparing three linear models in R.
- Mitsa, T. Cross-validation in R: a do-it-yourself and a black box approach. 22 May 2013. Accessed 14 May 2014. Shows how to use the package DAAG to calculate PRESS, or to calculate it manually.
- Walker, S. Calculating the PRESS statistic in R. 18 June 2013. ecology & stats. Accessed 14 May 2014. Provides a simple function for calculating PRESS in R.
- Multiple Regression Analysis: Use Adjusted R-Squared and Predicted R-Squared to Include the Correct Number of Variables
- Adjusted R-Square or Predicted R-Square. LinkedIn. Accessed 14 May 2014. Forum dscussion thread discusing the relative merits of adjusted and predicted R2, in which the equation for calculating predicted R2 is given.
- Why is adjusted R-squared less than R-squared if adjusted R-squared predicts the model better?. StackExchange. Accessed 10 May 2014. Q&A thread discussing the relative merits of R2 and adjusted R2.
- R Core Team (2014). R: A language and environment for statistical computing. R Foundation for
Statistical Computing, Vienna, Austria. URL http://www.R-project.org/. - H. Wickham. ggplot2: elegant graphics for data analysis. Springer New York, 2009.
Really great post, thanks! You might be interested in a new R package I’m development that uses the bootstrap to estimate a distribution of predictive R^2 statistics. To speed up the bootstrap, I’ve used C++ via Rcpp.
https://github.com/stevencarlislewalker/bootR2
Steve, thank you. That sounds like a great package; I’ll definitely have a look.
Reblogged this on Gabriel Rega.
Important article! Not wanting to do self-advertising ;-), but check the PRESS function in my ‘qpcR’ package that also works on nonlinear models where the “R-square” problem is even more severe,,,
Cheers,
Andrej
Hi, Indeed great post. Just one comment, I think that “The total sum of squares can be calculated directly as the sum of the squared residuals” is not accurate. I to obtain tss one should:
tss <- sum( ( x$y-mean( x$y ) )^2 )
Please forgive me if I misunderstood.
Both are correct. Your formula is how anova() calculates the “Sum sq” term, and is the sum of the squared residuals.
Tal is right: tss <- sum( ( x$y-mean( x$y ) )^2 ) is not the sum of squared residuals
I think that I see the confusion. It’s not the “residual sum of squares,” where RSS <- sum((x$y – f(x$x))^2). However, "sum of squared residuals" is accurate, though some authors (including Wikipedia) use "sum of squared residuals" as a synonym for "residual sum of squares." x$y – mean(x$y) is the residual for x$y, (x$y – mean(x$y))^2 is the square of the residual, and sum() of that is the sum of the square of the residuals.
Hi Tom,
Thanks for this great post – one question I have is what exactly the predicted r-square is measuring. I know its an effective measure of the predictive ability of the regression but would a value of e.g. 70% indicate that 30% of the time the model fails to provide a response that falls within the overall confidence interval of the model, or something else…?
It’s the goodness of fit of the actual values against the predicted values.